Research Summary

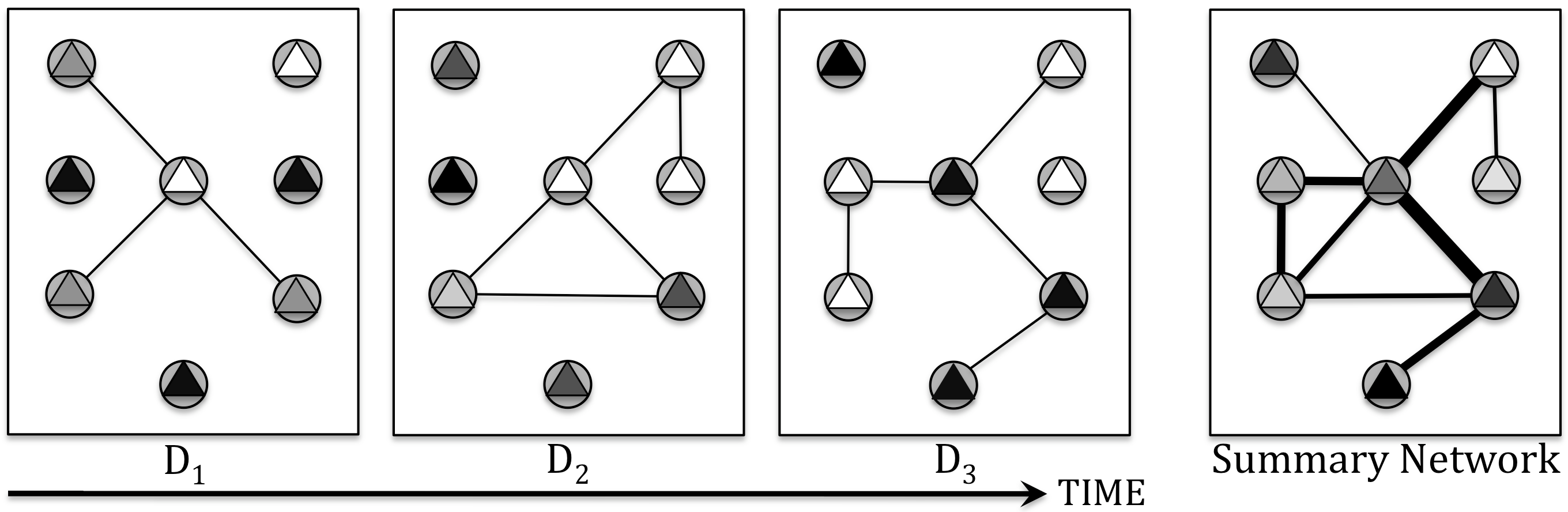
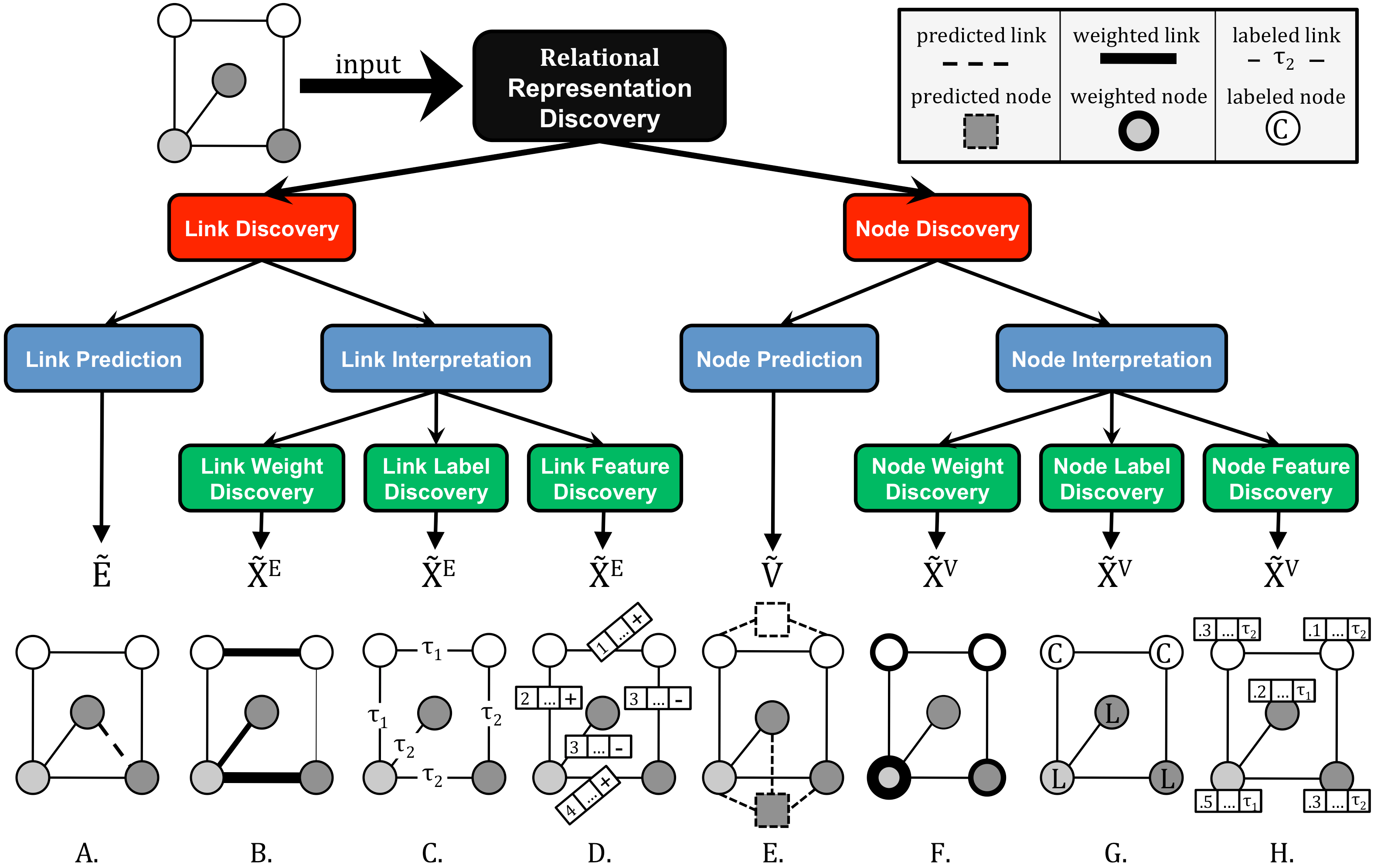
Relational data representations have become an increasingly important topic due to the recent proliferation of network datasets (e.g., social, biological, information networks) and a corresponding increase in the application of Statistical Relational Learning (SRL) algorithms to these domains. In this article, we examine and categorize techniques for transforming graph-based relational data to improve SRL algorithms. In particular, appropriate transformations of the nodes, links, and/or features of the data can dramatically affect the capabilities and results of SRL algorithms. We introduce an intuitive taxonomy for data representation transformations in relational domains that incorporates link transformation and node transformation as symmetric representation tasks. More specifically, the transformation tasks for both nodes and links include (i) predicting their existence, (ii) predicting their label or type, (iii) estimating their weight or importance (iv) systematically constructing their relevant features.

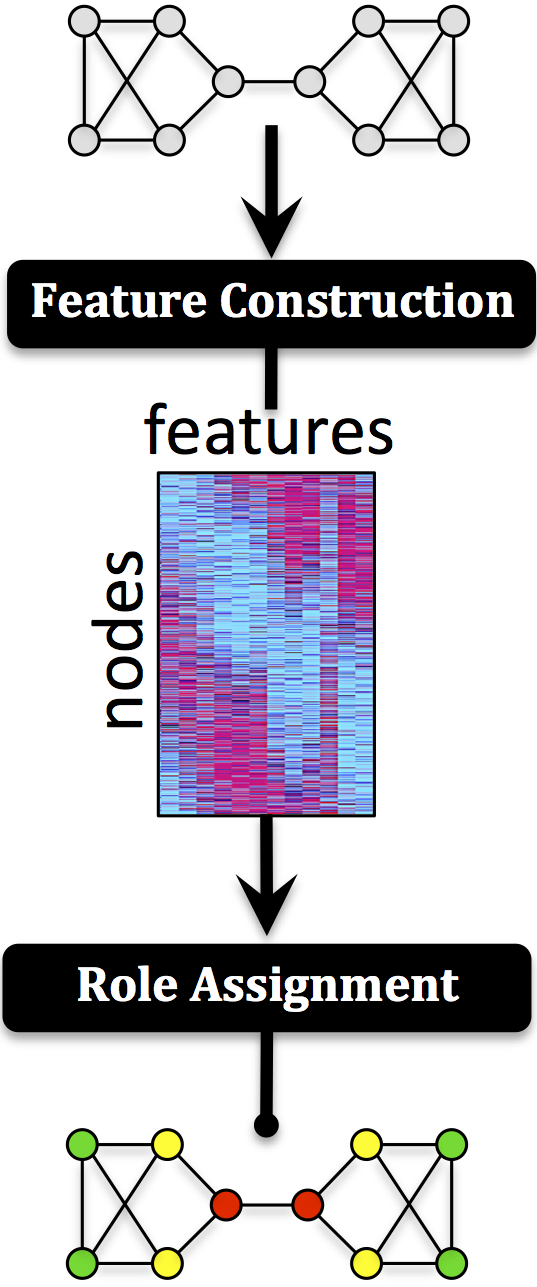
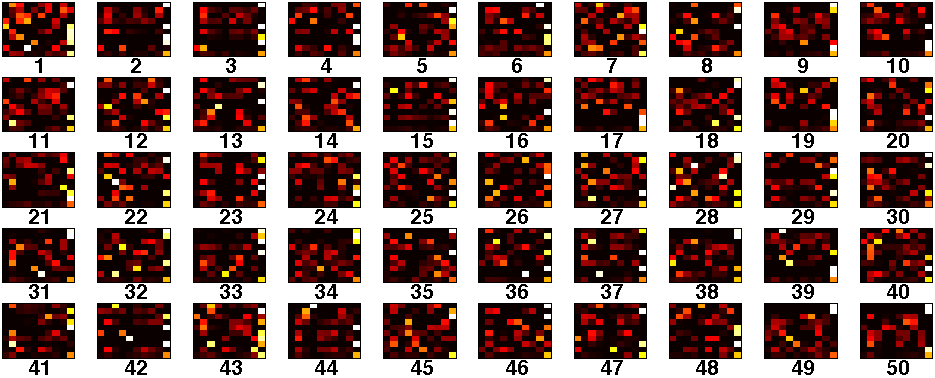
Roles represent node-level connectivity patterns such as star-center, star-edge nodes, near-cliques or nodes that act as bridges to different regions of the graph. Intuitively, two nodes belong to the same role if they are structurally similar. Roles have been mainly of interest to sociologists, but more recently, roles have become increasingly useful in other domains. Traditionally, the notion of roles were defined based on graph equivalences such as structural, regular, and stochastic equivalences. We briefly revisit these early notions and instead propose a more general formulation of roles based on the similarity of a feature representation (in contrast to the graph representation). This leads us to introduce a taxonomy of three general classes of techniques for discovering roles that includes(i) graph-based roles, (ii) feature-based roles, and (iii) hybrid roles. We also propose a flexible framework for discovering roles using the notion of similarity on a feature-based representation. The framework consists of two fundamental components: (a) role featureconstruction and (b) role assignment using the learned feature representation. We investigate the different possibilities for discovering feature-based roles and the tradeoffs of the many techniques for computing them.

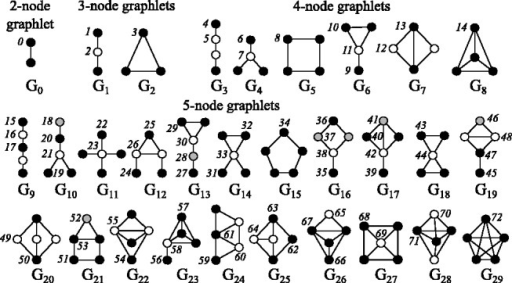
From social science to biology, numerous applications often rely on graphlets for intuitive and meaningful characterization of networks at both the global macro-level as well as the local micro-level. While graphlets have witnessed a tremendous success and impact in a variety of domains, there has yet to be a fast and efficient approach for computing the frequencies of these subgraph patterns. However, existing methods are not scalable to large networks with millions of nodes and edges, which impedes the application of graphlets to new problems that require large-scale network analysis. To address these problems, we propose a fast, efficient, and parallel algorithm for counting graphlets up to size k=4-nodes that take only a fraction of the time to compute when compared with the current methods used. The proposed graphlet counting algorithms leverages a number of proven combinatorial arguments for different graphlets. For each edge, we count a few graphlets, and with these counts along with the combinatorial arguments, we obtain the exact counts of others in constant time. On a large collection of 300+ networks from a variety of domains, our graphlet counting strategies are on average 460x faster than current methods. This brings new opportunities to investigate the use of graphlets on much larger networks and newer applications as we show in the experiments. To the best of our knowledge, this paper provides the largest graphlet computations to date as well as the largest systematic investigation on over 300+ networks from a variety of domains.

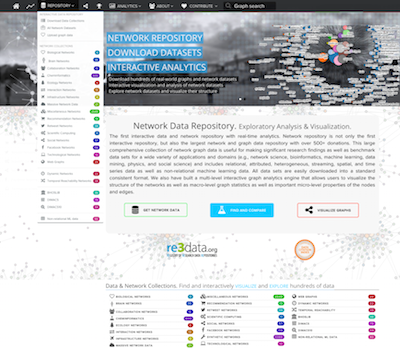
Scientific data repositories have historically made data widely accessible to the scientific community, and have led to better research through comparisons, reproducibility, as well as further discoveries and insights. Despite the growing importance and utilization of data repositories in many scientific disciplines, the design of existing data repositories has not changed for decades. This project revisits the current design and proposes the notion of interactive data repositories. These interactive data repositories move beyond traditional data repositories that focus on data accessibility by also providing techniques for interactive data exploration, mining, and visualization in an easy, intuitive, and free-flowing manner.